Question

Find the infinite limit

Answer 1

Since the function approaches ∞ from the left but -∞ from the right, the limit does not exist

Answer 2

`\displaystyle \lim_(x \to \infty) (√(x) + x^2)/(5x - x^2) = -1`

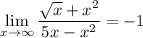
General Formulas and Concepts:

Calculus

Limits

Explanation:

We are given the following limit:

`\displaystyle \lim_(x \to \infty) (√(x) + x^2)/(5x - x^2)`

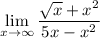
We can use the Coefficient Power Method to solve this. Since both the numerator and the denominator have the same power, we simply divide the coefficients to get our answer:

`\displaystyle \lim_(x \to \infty) (√(x) + x^2)/(5x - x^2) = (1)/(-1)`

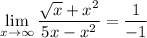
Simplifying it, we have:

`\displaystyle \lim_(x \to \infty) (√(x) + x^2)/(5x - x^2) = -1`

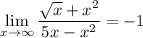
And we arrive at our answer.

Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Limits