Question

1. Graph Quadrilateral QUAD with the following coordinates. Q-8, 0, U0, 6, A8, 0, D(0, -15).QUAD is a __________ because it has exactly 2 pairs ofconsecutive _________ sides. Its diagonals are ___________.2. The perimeter of QUAD is __________________units.The area of QUAD is _______ units2.

Answer 1

Step-by-step explanation

Part 1.

We graph the quadrilateral QUAD. For this, we plot and join the given ordered pairs.

As we can see, the quadrilateral QUAD is a kite because it has exactly 2 pairs of consecutive congruent sides.

Part 2.

Finding the perimeter

The perimeter is the sum of the length of all the sides of a polygon. Then, to calculate the perimeter of the quadrilateral QUAD, we have to find the measure of the segments UA and AD. For this, we can use the distance formula between two points.

`\begin{gathered} d=√((x_2-x_1)^2+(y_2-y_1)^2) \\ \text{ Where }(x_1,y_1)\text{ and }(x_2,y_2)\text{ are the coordinates of the points.} \end{gathered}`

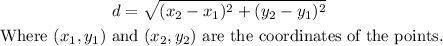
Then, we have:

• Measure of segment UA

`\begin{gathered} (x_1,y_1)=U(0,6) \\ (x_2,y_2)=A(8,0) \\ d=√((x_2-x_1)^2+(y_2-y_1)^2) \\ d=√((8-0)^2+(0-6)^2) \\ d=√(8^2+(-6)^2) \\ d=√(64+36) \\ d=√(100) \\ d=10 \end{gathered}`

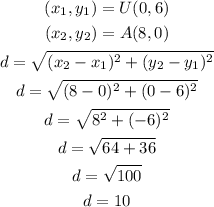
• Measure of segment AD

`\begin{gathered} (x_1,y_1)=A(8,0) \\ (x_2,y_2)=D(0,-15) \\ d=√((x_2-x_1)^2+(y_2-y_1)^2) \\ d=√((0-8)^2+(-15-0)^2) \\ d=√((-8)^2+(-15)^2) \\ d=√(64+225) \\ d=√(289) \\ d=17 \end{gathered}`

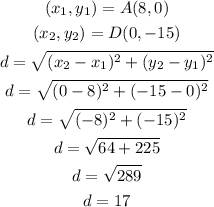
Now, we calculate the perimeter of the quadrilateral.

`\begin{gathered} \text{ Perimeter }=\bar{UA}+\bar{AD}+\bar{DQ}+\bar{QU} \\ \text{ Perimeter }=10+17+17+10 \\ \text{ Perimeter }=54 \end{gathered}`

Therefore, the perimeter of QUAD is 54 units.

Finding the area

The area of a kite is half the product of the lengths of its diagonals.

`A=(1)/(2)d_1*d_2`

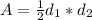
Then, we have to calculate the measure of segments UD and QA to find the area of the kite. For this, we can use the distance formula between two points.

• Measure of segment UD

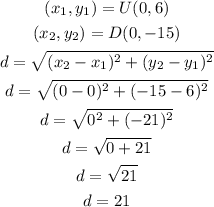
`\begin{gathered} (x_1,y_1)=U(0,6) \\ (x_2,y_2)=D(0,-15) \\ d=√((x_2-x_1)^2+(y_2-y_1)^2) \\ d=√((0-0)^2+(-15-6)^2) \\ d=√(0^2+(-21)^2) \\ d=√(0+21) \\ d=√(21) \\ d=21 \end{gathered}`

•