Question

If you graph both sides of the equation 2(2x + 3) = 4x + 6, what will the graph look like?

The graphs never intersect.
The graphs intersect at a single point.
The graphs are identical and intersect at infinitely many points.
The graphs intersect at exactly two points.

Answer 1

Distribute on the left
4x+6=4x+6

Because the equations are exactly the same, they are coinciding and all point intersect. Therefore, there are infinitely many solutions.

Final answer: C

Answer 2

The graphs are identical and intersect at infinitely many points.

Explanation:

Given the equation

`2(2x + 3) = 4x + 6`

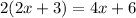
we have to compare the graph of both sides of equation.

`LHS: 2.(2x + 3)`

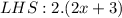
By distributive property,

`a.(b+c)=a.b+a.c`

`2.(2x + 3)=2.2x+2.3=4x+6`

`\text{The above expression implies 4x+6}`

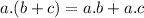
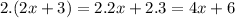
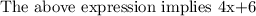
which is equals to RHS of given equation i.e

`4x+6=4x+6`

The both sides of equation are identical.

Since both sides of equation are identical therefore intersect at infinitely many points.

Option 3 is correct.