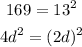Question

Factor 169-4d^2 and identify the perfect square

Answer 1

By definition, a Perfect square is a number that is the square of an Integer.

In this case, you have the following expression given in the exercise:

`169-4d^2`

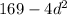
You can identify that:

`169=13\cdot13=13^2`

Therefore, it is a Perfect square.

Notice that:

`4d^2=(2d)^2`

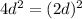
Therefore, it is a Perfect square.

For this case you must apply the Difference of two squares is:

`a^2-b^2=(a+b)(a-b)`

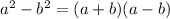
Then, you can factor the expression:

`=-(2d-13)(2d+13)`

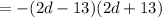
The answers are:

- Factored expression:

`-(2d-13)(2d+13)`

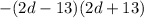
- ´Perfect squares:

`\begin{gathered} 169=13^2 \\ 4d^2=(2d)^2 \end{gathered}`