Question

What is the distance rounded to the nearest tenth between the points (2 -2) and (6 3)

Answer 1

The distance between the points is approximately 6.4

Explanation:

The given coordinates of the points are;

(2, -2), and (6, 3)

The distance between two points, 'A', and 'B', on the coordinate plane given their coordinates, (x₁, y₁), and (x₂, y₂) can be found using following formula;

`l = \sqrt{\left (y_(2)-y_(1) \right )^(2)+\left (x_(2)-x_(1) \right )^(2)}`

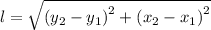
Substituting the known 'x', and 'y', values for the coordinates of the points, we have;

`l_((2, \, -2), \ (6, \, 3) ) = \sqrt{\left (3-(-2) \right )^(2)+\left (6-2 \right )^(2)} = √(5^2 + 4^2) = √(41)`

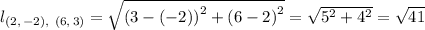
Therefore, the distance between the points, (2, -2), and (6, 3) = √(41) ≈ 6.4.