Question

A 490 mL IV bag contains a 20% dextrose solution. How much of the original solution must be replaced with a 65% dextrose solution to increase the original concentration to 45%? Round your final answer to 1 decimal place if necessary.

Answer 1

272.2 mL of 65% dextrose solution

EXPLANATION :

From the problem, we have to concentrations, 20% and 65% dextrose.

Let x = amount of 20% dextrose

y = amount of 65% dextrose

The sum of x and y is 490 mL, since it is the volume or space of the IV bag.

So we have :

`x+y=490`

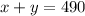
The resulting concentration must be 45%, so that will be :

`\begin{gathered} 0.20x+0.65y=0.45(490) \\ 0.20x+0.65y=220.5 \end{gathered}`

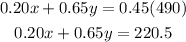
Now we have two equations two unknowns.

Express the first equation as x in terms of y :

`\begin{gathered} x+y=490 \\ x=490-y \end{gathered}`

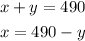
Substitute x to the second equation :

`\begin{gathered} 0.20(490-y)+0.65y=220.5 \\ 98-0.20y+0.65y=220.5 \\ 0.45y=220.5-98 \\ 0.45y=122.5 \\ y=(122.5)/(0.45) \\ y=272.2 \end{gathered}`

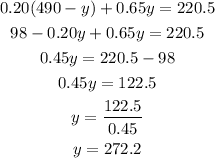
So we have y = 272.2 mL.

It needs 272.2 mL of 65% dextrose solution.