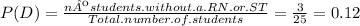Question

Sore ThroatNo Sore Throat612Runny Nose43No Runny NoseSend datato Excel(a) Find the probability that a randomly selected student has a runny nose.(b) Find the probability that a randomly selected student has a sore throat.(C) Find the probability that a randomly selected student has a runny nose or a sore throat.(d) Find the probability that a randomly selected student has neither runny nose nor a sore throat.

Answer 1

To calculate the probabilities asked you need to calculate the margins of the table, i.e. the total numbers of each colum and row, and the total of observations.

To calculate all asked probabilities you have to divide the number of students that have the condition you are interested by the total of students observed by the nurse:

`P=(nºsuccesses)/(Total.number.of.students)`

a) You have to find the probability that a randomly selected student has a runny nose (RN). For this you have to use the margin of the table and divide the total number of students that had a runny nose by the total of students observed by the nurse:

`P(RN)=(nºstudents.with.RunnyNose)/(Total.of.students)=(18)/(25)=0.72`

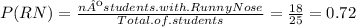
b) To find the probability of randomly selecting a student with sore throat (ST), following the same method as before, you have to work with the total of students observed that had a soar throat and divide it by the total of students.

`P(ST)=(nºstudents.withSoreThroat)/(Total.of.students)=(10)/(25)=0.4`

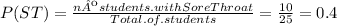
c) In this item you have to calculate the probability that the student has a runny nose or a sore throat.

For the student to present "Runny Nose" or "Sore throat", this determines a union between these two events.

To calculate the union of two non mutually exclusive events you have to follow the rule:

`P(A\cup B)=P(A)+P(B)-P(A\cap B)`

Since there are elements in common for both events, you are counting the students that have both a runny nose and a sore throat twice, so you have to subtract this intersection once to reach the correct probability value.

I'll call this probability P(C)

`\begin{gathered} P(C)=P(RN\cup ST) \\ P(RN)+P(ST)-P(RN\cap ST) \\ (18)/(25)+(10)/(25)-(6)/(25)=(22)/(25)=0.88 \\ \end{gathered}`

The probability is P(C)=0.88

d) To calculate the probability of the randonmly selected student to have neither state, you have to divide the total number of students that had no sore throat and no runny nose by the total number of students.

I'll call it P(D)

`P(D)=(nºstudents.without.a.RN.or.ST)/(Total.number.of.students)=(3)/(25)=0.12`