Question

What is the length of a hypothesis if necessary round to the nearest tenth

Answer 1

Answer: 17

Step-by-step explanation:

We have a right triangle (a triangle with an angle of 90°). To find the value of c (the hypotenuse of the triangle) we use the Pythagorean theorem:

Where a and b are the legs of the triangle and c is the hypotenuse.

In this case, the value of a and b is:

`\begin{gathered} a=8cm \\ b=15cm \end{gathered}`

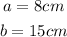
Substituting these values into the Pythagorean theorem formula:

`c^2=(8cm)^2+(15cm)^2`

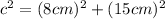
Solving the operations:

`\begin{gathered} c^2=64cm^2+225cm^2 \\ \downarrow \\ c^2=289cm^2 \end{gathered}`

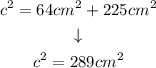
Solving for c:

`c=\sqrt[]{289cm^2}`

the result is:

`c=17cm`

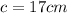
Answer: 17