Question

Find the value of x that makes A || B.2435.2 = 3x - 20 and 25 = x + 20x = [?]

Answer 1

Given:

`\begin{gathered} \angle2=3x-20 \\ \angle5=x+20 \end{gathered}`

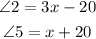
For line A and line B to be parallel lines, then the measure of angle 2 must be equal (congruent) to the measure of angle 5.

Thus,

`\angle2\cong\angle5`

If angle 2 and angle 5 are congruent, then A || B.

Angle 2 and angle 5 are corresponding angles when A || B.

Corresponding angles are formed when a transversal passes through two lines. The angles that are formed in the same position, in terms of the transversal, are corresponding angles. Corresponding angles are congruent.

Hence,

`\begin{gathered} \angle2=\angle5\ldots\ldots\ldots\ldots\ldots\text{.Corresponding angles are congruent} \\ 3x-20=x+20 \\ \text{Collecting the like terms to solve for x,} \\ 3x-x=20+20 \\ 2x=40 \\ \text{Dividing both sides by 2,} \\ x=(40)/(2) \\ x=20 \end{gathered}`

Therefore, the value of x that makes A || B is 20