Given:
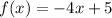
Required:
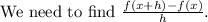
Step-by-step explanation:
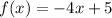
Replace x =x+h in the function f(x).
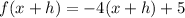

Substract the function f(x) from f(x+h).

Distribute minus sign.
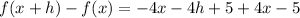
add the like terms which are like with the same variable with the same power.
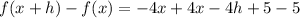

Divide both sides of the equation by h.
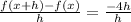
Cancel out the common multiple h.

Final answer:
