Explanation:
The given expression is
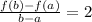
Notice that
 and
and
 are elements of the domain and
are elements of the domain and
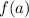 and
and
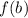 are elements of the range.
are elements of the range.
Observe the notation used, an element of the range is always written like
 where
where
 is an element of the domain.
is an element of the domain.
Also, notice that this expression is using two pair of coordinates, which are
 and
and
 .
.
On the other hand, the definition of average rate of change is

Where
 and
and
 .
.
Having said that, the given expression represents an average rate of change in the interval, where the rate is 2. The right answer is the third option.