128 children and 175 adults
Step-by-step explanation
Step 1
Set the equations:
a)
Let x represents the number of children
Let y represents the number of adults
On a certain day, 303 people entered the park,so
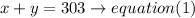
b) total collected: $3,329.00
the fee for a children is 5.50, so the money from the children fee is = x*5.5=5.5x
the fee for a children is 15, so the money from the children fee is = y*15=15y
if the total is $3,329.00
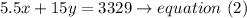
Step 2
solve the equations:
a) isolate x in equation (1) and replace in equation(2)

now,replace in equation (2)

hence,
the number of admitted adults is 175
b)finally, replace the y value in equation (3)
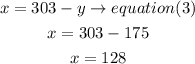
so, the number of admitted children is 128
I hope this helps you