Answer:
£1,120
Explanation:
The computation of the total money earned is given below:
Given that
Ratio of children to adult be 2;3
There is 80 children
each adult cost is £8
And for children it is quarter of adult i.e £8 ÷ 4 = £2
For children there is an earning of
= 80 × £2
= £160
And, for adult it would be
but before that the number of adults be
Let us assume the number of adults be x
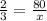
After cross multiplication, the number of adult be 120
So the adult earning be
= 120 × £8
= £960
So, the total money made would be
= £960 + £160
= £1,120