Question

Hi, can you help me answer this question please, thank you!

Answer 1

Before we begin solving this question, we need to know a couple of things:

1. What are the sample proportions (i.e. probability of success) for the two samples.

2. What is the proportion difference claimed by the question.

3. How many tails is this test going to be?

4. What is the mean sample proportion for both samples?

The answers to thesee questions can be inferre from the question.

1. The sample proportions are:

`\begin{gathered} p_1=(122)/(202)=(61)/(101) \\ \\ P_2=(220)/(340)=(11)/(17) \end{gathered}`

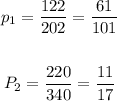
2. The proportion difference is gotten as follows:

`\begin{gathered} D_0=p_1-p_2 \\ \text{ But we know from the question that the claim or Null Hypothesis is:} \\ p_1=p_2 \\ p_1-p_2=0 \\ \\ \therefore D_0=0 \end{gathered}`

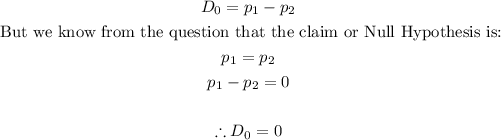
Thus, the proportion difference is 0.

3. The number of tails in the test is determined by the Alternate hypothesis. Since the alternate hypothesis only cares about when p1 is greater than p2, and not the region when p1 is less than p2, that means that we are only concerned with a ONE-TAILED TEST.

4. The mean sample proportion for both samples is given as follows:

`\begin{gathered} \bar{p}=(s_1+s_2)/(n_1+n_2) \\ \text{where,} \\ s_1=\text{ the number of successes of sample one} \\ s_2=\text{ The number of successes of sample two.} \\ \\ \therefore\bar{p}=(122+220)/(202+340)=(342)/(542)=(171)/(271) \end{gathered}`

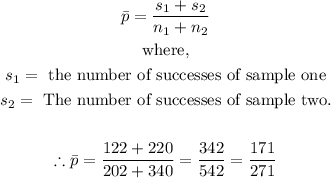
Now, we can proceed to solve the question.

Test-Statistic:

The test statistic for comparing two proportion samples is gotten using the formula given below:

`\begin{gathered} Z_{\text{stat}}=\frac{(\bar{p_1}-\bar{p_2})-D_0}{\sqrt[]{\bar{p}(1-\bar{p})((1)/(n_1)+(1)/(n_2))}} \\ \\ \text{where,} \\ \bar{p}=\text{proportion for sample one} \\ \bar{p}=\text{proportion for sample two} \\ \bar{p}=mean\text{ proportion for both samples} \\ n_1=\text{ Number of people in sample one} \\ n_2=\text{ Number of people in sample two} \end{gathered}`

This is a Z-statistic because the number of samples is greater than 30.

We have all the parameters, thus, let us calculate our test statistic.