Answer:
The area of the square is 1.266
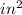 less than the circle.
less than the circle.
Explanation:
The area of a square is given by the formula
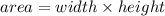
But since the width and height are by definition the same, the formula is usually written as

where s is the length of one side.
Given the radius of a circle, the area inside it can be calculated using the form
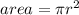
where r is the radius of the circle and
 is Pi, approximately 3.142.
is Pi, approximately 3.142.
So, the area of a square with a side length of 7 inches is
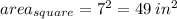
the area of a circle with a radius of 4 inches is
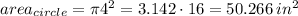
Now, we take the difference in the areas.
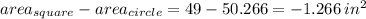
Because the difference between the areas of the square and the circle is negative, the area of the square is 1.266
 less than the circle.
less than the circle.