Question

HELP PLEASE

(a) What is wrong with the following equation?

x2 + x − 42/ x − 6 = x + 7

1)(x − 6)(x + 7) ≠ x2 + x − 42
2)The left-hand side is not defined for x = 0, but the right-hand side is.
3)The left-hand side is not defined for x = 6, but the right-hand side is.
4)None of these — the equation is correct.

Answer 1

`\bf \cfrac{x^2-x-42}{x-6}\implies \cfrac{(x+7)\underline{(x-6)}}{\underline{x-6}}\implies x+7`

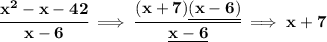
so.. the left-hand-side does indeed simplify to x+7, so the equation does check out.

however, notice something, for the equation of x+7, when x = 6, we get (6) + 7 which is 13.

BUT for the rational, we get
`\bf \cfrac{x^2-x-42}{x-6}\qquad \boxed{x=6}\implies \cfrac{x^2-x-42}{\boxed{6}-6}\implies \stackrel{und efined}{\cfrac{x^2-x-42}{0}}`

so, even though the siimplification is correct, the rational or original expression is constrained in its domain.