Question

the plant growth is proportional in time when Tia brought the plant it measured 2 cm it measured 2.5 cm exacly one week later if the plant continues to grow at this rate determine the function that represents the plants growth.2nd part:how many weeks have passed if the plant is 18 cm tall?

Answer 1

The initial height if the plant is: 2 cm

After 1 week, the height of the plant is: 2.5 cm

Step 1. Find the difference in the height of the plant from the initial height to the height after 1 week:

`2.5-2=0.5`

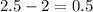
The rate at which the plant grows is 0.5 cm per week.

Step 2. Determine the function that represents the growth of the plant.

First, let's define our variables:

x--> Number of weeks

y--> Height of the plant

Since the starting height is 2cm and the plant grows 0.5 per week:

`y=2+0.5x`

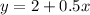
Where 2 is the initial height, 0.5x is the growth after x number of weeks, and y is the height of the plant after x weeks.

Step 3. To solve the second part of the problem we need to find the number of weeks that have passed when the plant is 18cm tall.

Remember that we defined "y" as the height of the plant, so:

`y=18`

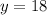
Now, substitute y=18 into our equation found in step 2:

`\begin{gathered} y=2+0.5x \\ 18=2+0.5x \end{gathered}`

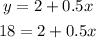
And now solve for the number of weeks "x".

To solve for x, subtract 2 to both sides of the equation:

`\begin{gathered} 18-2=2-2+0.5x \\ 16=0.5x \end{gathered}`

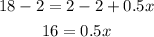
And divide both sides of the equation by 0.5:

`\begin{gathered} (16)/(0.5)=(0.5x)/(0.5) \\ 32=x \end{gathered}`

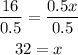
32 weeks have passed.

Answer:

Function:

`y=2+0.5x`

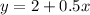
and

how many weeks have passed if the plant is 18 cm tall? 32 weeks.