Question

The points P(0,5)(0,5), Q(0,-3)(0,−3), R(9,-8)(9,−8), and S(9,0)(9,0) form parallelogram PQRS. find the perimeter of the parallelogram. Round your answer to the nearest tenth if necessary.

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given vertices

`\begin{gathered} P(0,5) \\ Q(0,-3) \\ R(9,-8) \\ S(9,0) \end{gathered}`

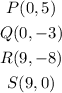
STEP 2: Draw the plot

STEP 3: Find the measure of PQ

`\begin{gathered} \mathrm{Compute\:the\:distance\:between\:}\left(x_1,\:y_1\right),\:\left(x_2,\:y_2\right):\quad √(\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2) \\ \mathrm{The\:distance\:between\:}\left(0,\:5\right)\mathrm{\:and\:}\left(0,\:-3\right)\mathrm{\:is\:} \\ =√(\left(0-0\right)^2+\left(-3-5\right)^2) \\ =8 \end{gathered}`

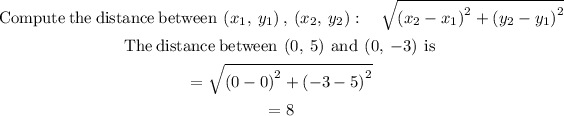
STEP 4: Find the measure of PS

`\begin{gathered} \mathrm{Compute\:the\:distance\:between\:}\left(x_1,\:y_1\right),\:\left(x_2,\:y_2\right):\quad √(\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2) \\ \mathrm{The\:distance\:between\:}\left(0,\:5\right)\mathrm{\:and\:}\left(9,\:0\right)\mathrm{\:is\:} \\ =√(\left(9-0\right)^2+\left(0-5\right)^2) \\ =√(106) \end{gathered}`

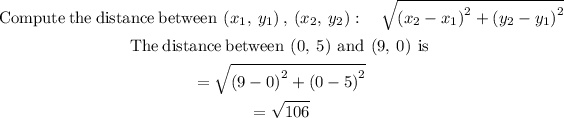
STEP 5: Find the measure of QR

`\begin{gathered} \mathrm{Compute\:the\:distance\:between\:}\left(x_1,\:y_1\right),\:\left(x_2,\:y_2\right):\quad √(\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2) \\ \mathrm{The\:distance\:between\:}\left(0,\:-3\right)\mathrm{\:and\:}\left(9,\:-8\right)\mathrm{\:is\:} \\ =√(\left(9-0\right)^2+\left(-8-\left(-3\right)\right)^2) \\ =√(106) \end{gathered}`

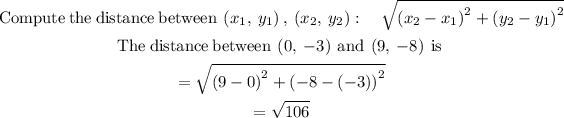
STEP 5: Find the measure of RS

`\begin{gathered} \mathrm{The\:distance\:between\:}\left(9,\:-8\right)\mathrm{\:and\:}\left(9,\:0\right)\mathrm{\:is\:} \\ =√(\left(9-9\right)^2+\left(0-\left(-8\right)\right)^2) \\ =8 \end{gathered}`

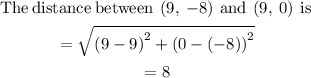
STEP 6: Find the perimeter of the parallelogram

`\begin{gathered} Perimeter=2(a+b) \\ a=8,b=√(106) \\ Perimeter=2(8+√(106)) \\ \mathrm{Apply\:the\:distributive\:law}:\quad \:a\left(b+c\right)=ab+ac \\ 2\left(8+√(106)\right)=2\cdot\:8+2√(106) \\ =2\cdot \:8+2√(106) \\ =16+2√(106) \\ =36.59126028 \\ Perimeter\approx36.6 \end{gathered}`

Hence, the perimeter of the parallelogram is 36.6