Question

solve: The length of a rectangular room is 4 feet longer than twice its width. If the room’s perimeter is 164 feet, what are the room dimensions?

Answer 1

length: 56ft

width: 26ft

Explanation:

Given:

width = w

length = 4 + 2w

The perimeter is the sum of all the sides of the rectangle, therefore:

`\begin{gathered} w+l+w+l=164 \\ 2w+2l=164 \\ \text{ we replacing and solving for w:} \\ 2w+2\cdot(4+2w)=164 \\ 2w+8+4w=164 \\ 6w=164-8 \\ w=(156)/(6) \\ w=26\text{ ft} \end{gathered}`

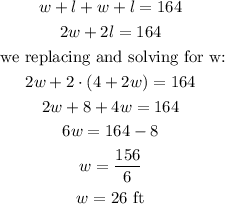
Now, since the length is a function of the width, we can calculate it like this:

`\begin{gathered} l=4+2\cdot26 \\ l=4+52 \\ l=56\text{ ft} \end{gathered}`

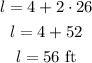
Therefore, the dimensions of the room are 26 feet wide and 56 feet long.