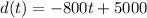Question

a plane is currently 5000 KM from its distance. 1.5 hours later, it is 3800 KM from it's distance. develope a linear model for the distance D remaining after T hours of travelintercept the gradientinterpret the D and T interceptsState a reasonable domain and range for your model

Answer 1

Step-by-step explanation

The first point corresponds to (0,5000) because for 0 hours its 5000 km from its distance.

The second point corresponds to (1.5 , 3800) because after 1.5 hours its 3800 k from its distance.

Lets graph this points:

The line passing through these points is the model we need for the situation.

We have the y-intercept at (0,5000) and the slope of this function is:

`\begin{gathered} (5000-3800)/(0-1.5) \\ (1200)/(-1.5) \\ -800 \end{gathered}`

Then the linear model must be:

`d(t)=-800t+5000`

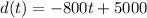
The distance decreases 800 km every hour.

Range: [0,5000]

Domain:[0,6.25]

The domain is from 0 to 6.25 because after 6.25 hours that plane will be on the ground.

Answer

Range: [0,5000]

Domain:[0,6.25]

Linear model:

`d(t)=-800t+5000`