Given the polynomial:
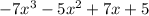
Let's use the Factor Theorem to determine whether x + 1 is a factor of the polymomial above.
The Factor Theorem states that for an x+1 to be a factor of the polyomial, x = -1 must be a zero of f(x).
Let's use synthetic division to divide the polynomials. If the remainder is 0, then x + 1 is a factor of the polynomial.
x + 1
Rewrite the expression for x:
x + 1 - 1 = 0 - 1
x = -1
To use synthetic division, take the following steps:
• Place the coefficients representing the divisor and the dividend into a division-like configuration.
• Add the product of the multiplication and the number from the dividend and put the result in the next position on the result line.
• Multiply the newest result by the divisor an put the result under the next term in the dividend.
The last value on the line is the remainder.
Hence, the remainder here is = 0.
Since the remainder is 0, the Factor Theorem states that x + 1 is a factor of the given polynomial.
Yes, x+1 is a factor of the given polynomial.
ANSWER:
Yes