Question

The drama club is selling tickets to their play to raise money for the show's expenses.Each student ticket sells for $5 and each adult ticket sells for $7.50. The auditoriumcan hold at most 125 people. The drama club must make no less than $790 fromticket sales to cover the show's costs. If 73 adult tickets were sold, determine allpossible values for the number of student tickets that the drama club must sell inorder to meet the show's expenses. Your answer should be a comma separated list ofvalues. If there are no possible solutions, submit an empty answer.

Answer 1

Let

x ------> number of student tickets that the drama club must sell

so

we have

`x+73\leq125`
`\begin{gathered} x\leq125-73 \\ x\leq52 \end{gathered}`

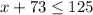
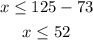
and

`5x+7.50\cdot73\ge790`
`\begin{gathered} 5x\ge790-547.5 \\ 5x\ge242.5 \\ x\ge48.5 \end{gathered}`

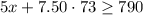
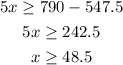
the values of x lie on the interval [48.5,52]

therefore

all possible values for the number of student tickets are on the interval

[49,52]

Integers greater than or equal to 49 and less than or equal to 52

possibles values are 49,50,51,52