We are told that BF is parallel to CD. From the figure we can also see that GC is parallel to FE.
Let's beggin by noting that ∠1 is formed by the intersection between lines BF, AH and GC. Since BF is parallel to CD, FE is parallel to GC and AH also intersects them, let's see if we can find similarities between these two sections
We can observe that, going clockwise, the angle after ∠1, ∠2 and ∠5 is a vertical angle of ∠1, so it it also 70.
Likewise, the angle after ∠3, ∠4 and ∠6 is a vertical angle of ∠3, so they are the same.
With this, we have the equation
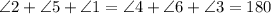
Let's note that ∠6+∠4 is the one we are trying to find.
From the figure, since ∠2 is formed by the intersection of GC and BF, it will be congruent with ∠4, since it is formed by the intersection of lines parallel to the ones that form ∠2.
Likewise, since ∠5 is formed by the intersection of GC and AH, it is congruent with ∠6, which is formed by the same line AH and a line parallel to GC.
This reduces our previous equation to this:
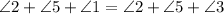
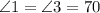
From here, let's return to our first equation:
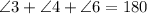
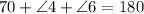
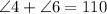
Therefore, m∠CDH=110