Answer:
The distance from the flagpole to the tree is 27 ft
Explanation:
Similar Triangles
Since the elevation angle from which the trees cast their shadows has the same measure and given the tree and the flagpole and the ground form right angles, both triangles are similar.
Similar triangles have their corresponding side lengths proportional. The ratio between the distances from the bench to the tree and flagpole and their heights is constant, i.e.:
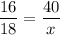
Where x is the distance from the bench to the tree.
Solving for x:
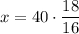
x = 45 feet
Thus the distance from the flagpole to the tree is 45 - 18 = 27 feet