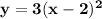Question

Given the vertex (2,0) and the point on the parabola (1, 3) find the quadratic equation

Answer 1

`y=3(x-2)^2`

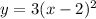
Explanation:

The vertex form of the quadratic function has the following equation:

`y=a(x-h)^2+k`

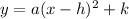
Where (h, k) is the vertex of the parabola, and a is a coefficient different from zero.

We are given the vertex located at (2,0). The equation is now:

`y=a(x-2)^2+0`

`y=a(x-2)^2`

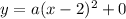
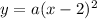
Since we know the point (1,3) is on the parabola:

`3=a(1-2)^2`

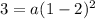
3=a(1)

a = 3

Finally, the quadratic equation is:

`\mathbf{y=3(x-2)^2}`