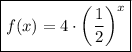Answer:
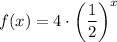
Explanation:
Exponential Function
The exponential function can be written with the general equation:
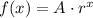
Where A is the value when x=0 and r>0 is the ratio. If r is greater than 1, the function is increasing, if r is less than 1, the function is decreasing.
The table shows the relation between values of x and values of the function y. Note that as x increases (one by one), y decreases with a ratio of 1/2. Only the last two choices have ratios of r=1/2. We only have to test which one of them has the correct value of y=4 when x=0.
Substituting in the third function:
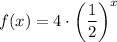
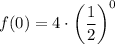
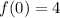
This gives the correct value of f(0)=4.
Substituting in the fourth function:
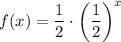

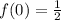
This choice is wrong
Correct choice: