Question

Please help!!

Find the explicit rule:

Answer 1

The explicit rule of the given sequence is a
`_(n)` = -84 + 7n

Explanation:

The nth term of the arithmetic sequence is a
`_(n)` = a + (n - 1)d, where

• a is the first term

• d is the common difference between each 2 consecutive terms

∵ a
`_(11)` = -7

∴ n = 11

→ Substitute n by 11 in the nth term rule

∴ a
`_(11)` = a + 10d

→ Equate the right sides of a
`_(11)`

∴ a + 10d = -7 ⇒ (1)

∵ a
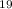`_(19)` = 49

∴ n = 19

→ Substitute n by 19 in the nth term rule

∴ a
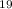`_(19)` = a + 18d

→ Equate the right sides of a
`_(19)`

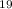
∴ a + 18d = 49 ⇒ (2)

→ Subtract equation (1) from equation (2)

∵ (a - a) + (18d - 10d) = (49 - -7)

∴ 0 + 8d = (49 + 7)

∴ 8d = 56

→ Divide both sides by 8 to find d

∴ d = 7

→ Substitute the value of d in equation (1) to find a

∵ a + 10(7) = -7

∴ a + 70 = -7

→ Subtract 70 from both sides

∵ a + 70 - 70 = -7 - 70

∴ a = -77

→ Substitute the values of a and d in the rule of the nth term above

∵ a
`_(n)` = -77 + (n - 1)(7)

∴ a
`_(n)` = -77 + (n)(7) - (1)(7)

∴ a
`_(n)` = -77 + 7n - 7

∴ a
`_(n)` = -84 + 7n

∴ The explicit rule of the given sequence is a
`_(n)` = -84 + 7n