Answer:
The concentration of Bromine is 0.308M
The concentration of Iodine is 0.308M
Step-by-step explanation:
From the question, we are given the following parameters:
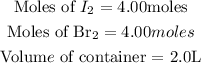
Get the concentration of Iodine and Bromine
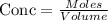
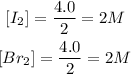
Given the chemical reaction between Iodine and Bromine;
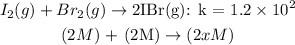
From the equation, we can see that there is no concentration for the molecule 2IBr, so we can give it "2x"
According to the equilibrium constant formula:
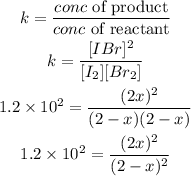
Simplify the result to get the value of "x"
![\begin{gathered} 1.2*10^2=((2x)/(2-x))^2 \\ 120=((2x)/(2-x))^2 \\ \sqrt[]{120}^{}=(2x)/(2-x) \\ 10.9544=(2x)/(2-x) \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/chemistry/college/nejxpimsabv5avppchpz.png)
Cross multiply and simplify
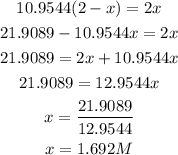
Get the concentration of the entities in the mixture
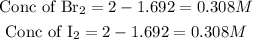
Hence the equilibrium concentrations of all entities in the mixture are 0.308M of Bromine and 0.308M of Iodine