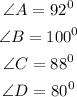Solution:
Given:
To solve the angle, we use the theorem of angles in a cyclic quadrilateral.
The theorem states that the opposite angles in a cyclic quadrilateral are supplementary (i.e. they add up to 180°).
Hence,
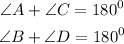
Thus,
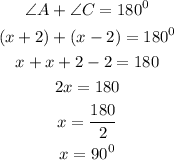
Hence,

Therefore, the measure of each angle of the quadrilateral is;