Question

Use the graph below to answer the question that follows:

What trigonometric function represents the graph? (6 points)
Select one:
a. f(x) = −3 sin(x − pi over 2 )
b. f(x) = −3 cos(x − pi over 2 )
c. f(x) = 3 cos(x − pi over 2 )
d. f(x) = 3 sin(x − pi over 2 )

Answer 1

Hello,


`if\ x=0\ then \\ a)f(x)=-3*sin(-(\pi)/(2))=-3*(-1)=3\ and\ not \ 0\\ d)f(x)=3*sin(-(\pi)/(2))=3*(-1)=-3\ and\ not \ 0\\ \\\\ if\ x= (\pi)/(2) \ then\ \\ b)f(x)=-3*cos(0)=-3\ and\ not\ 3\\`

So answer C

Answer 2

The trigonometric function which represents the graph is:

c)
`f(x)=-3\cos (x-(\pi)/(2))`

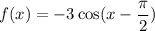
Explanation:

From the graph we may observe that when x=π/2 we have the value of the function f(x)= 3

Hence, we will check in which this point hold true:

a)

`f(x)=-3\sin (x-(\pi)/(2))`

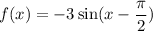
Now, when x=π/2 we have:

`f(x)=-3\sin ((\pi)/(2)-(\pi)/(2))\\\\\\f(x)=-3\sin (0)\\\\\\f(x)=0\\eq 3`

Hence, option: a is incorrect.

b)

`f(x)=-3\cos (x-(\pi)/(2))`

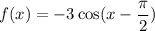
Now, when x=π/2 we have:

`f(x)=-3\cos ((\pi)/(2)-(\pi)/(2))\\\\\\f(x)=-3\cos (0)\\\\\\f(x)=-3\\eq 3`

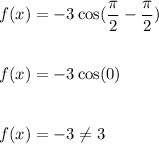
Hence, option: b is incorrect.

d)

`f(x)=3\sin (x-(\pi)/(2))`

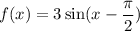
Now, when x=π/2 we have:

`f(x)=3\sin ((\pi)/(2)-(\pi)/(2))\\\\\\f(x)=3\sin (0)\\\\\\f(x)=0\\eq 3`

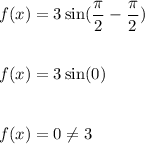
Hence, option: d is incorrect.

c)

`f(x)=-3\cos (x-(\pi)/(2))`

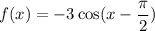
Now, when x=π/2 we have:

`f(x)=3\cos ((\pi)/(2)-(\pi)/(2))\\\\\\f(x)=3\cos (0)\\\\\\f(x)=3`

Similarly we will see that the value of this function matches all the points that on the graph.

Hence, option: c is correct.