Question

What is the perimeter of △LMN?

A. 8 units
B. 9 units
C. 6 + √10 units
D. 8 + √10 units

Answer 1

I solved this via the Pythagorean theorem. Side LM is 5 and side NM is 3.16. Side NL is also 3. 3+5+3.16=11.16. The decimal form of 8+sqrt(10) is 11.16. D is the answe

Answer 2

we know that

The distance 's formula between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

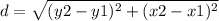
Step
`1`

Find the distance MN

`M(-2,1)\\N(-1,4)`

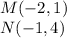
Substitute in the distance's formula

`d=\sqrt{(4-1)^(2)+(-1+2)^(2)}`

`d=\sqrt{(3)^(2)+(1)^(2)}`

`dMN=√(10)\ units`

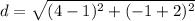
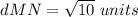
Step
`2`

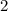
Find the distance NL

`N(-1,4)\\L(2,4)`

Substitute in the distance's formula

`d=\sqrt{(4-4)^(2)+(2+1)^(2)}`

`d=\sqrt{(0)^(2)+(3)^(2)}`

`dNL=3\ units`

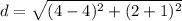
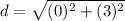
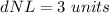
Step
`3`

Find the distance LM

`L(2,4)\\M(-2,1)`

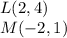
Substitute in the distance's formula

`d=\sqrt{(1-4)^(2)+(-2-2)^(2)}`

`d=\sqrt{(-3)^(2)+(-4)^(2)}`

`dLM=5\ units`

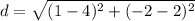
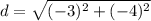
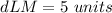
Step
`4`

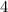
Find the perimeter of the triangle LMN

we know that

The perimeter of a triangle is equal to the sum of the three length sides

In this problem

`Perimeter=MN+NL+LM`

substitute the values in the formula

`Perimeter=(√(10)+3+5)\ units`

`Perimeter=(8+√(10))\ units`

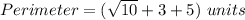
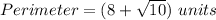
therefore

the answer is the option D

the perimeter of the triangle LMN is equal to
`(8+√(10))\ units`