Question

1.  Lisa is working with the system of equations x + 2y = 7 and 2x ‒ 5y = 5. She multiplies the first equation by 2 and then subtracts the second equation to find 9y = 9, telling her that y = 1. Lisa then finds that x = 5. Thinking about this procedure, Lisa wonders:

There are lots of ways I could go about solving this problem. I could add 5 times the first equation and twice the second or I could multiply the first equation by ‒2 and add the second. I seem to find that there is only one solution to the two equations but I wonder if I will get the same solution if I use a different method?

What is the answer to Lisa’s question? Explain.

2.   Does the answer to the first question change if we have a system of two equations in two unknowns with no solutions? What if there are infinitely many solutions?

Answer 1

All methods are supposed to be correct in most if not all situations and it should not matter if you use a different method given the options

Answer 2

1. Yes

2. Yes

Explanation:

1. Lets test Lisa's different solution. Lets times 5 to the first equation:

`5\cdot{x}+10\cdot{y}=35`

and 2 times the second equation:

`4\cdot{x}-10\cdot{y}=10`

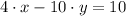
lets add the two equations:

`9\cdot{x}=45`

`x=5`

The second method is multiplying the first equation by -2:

`-2\cdot{x}-4\cdot{y}=-14`

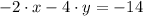
and add the second equation:

`-9\cdot{y}=-9`

`y=1[tex]</p><p>Substitute into equation 1:</p><p>[tex]x+2\cdot{1}=7`

`x=5`

The answer to Lisa's question is yes she wull get the same solution if she uses a different method.

2. Yes, The answer would change if the same amout of x and y values are the same and therefore we cannot solve for x and y. If there was infinitely many solutions we would have quadratic equations.