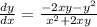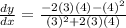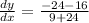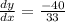Question

For the curve xy(x+y)=84, find dy/dx at (3,4)

Answer 1

implicit differentiation, yeah

hmm, never seen derivitive of 3 of them before

let's distribute

x²y+xy²=84
implicit differntiation

remember, dy/dx f(x)g(x)=f'(x)g(x)+f(x)g'(x)
and dy/dx y=dy/dx

so
2xy+x² dy/dx+y²+2xy dy/dx=0
solving for dy/dx
minus (2xy+y²) from both sides
x² dy/dx +2xy dy/dx=-2xy-y²
undistribute dy/dx
dy/dx(x²+2xy)=-2xy-y²
divide both sides by (x²+2xy)

`(dy)/(dx)=(-2xy-y^2)/(x^2+2xy)`

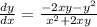
at (3,4)
evalaute for x=3 and y=4


`(dy)/(dx)=(-2xy-y^2)/(x^2+2xy)`

`(dy)/(dx)=(-2(3)(4)-(4)^2)/((3)^2+2(3)(4))`

`(dy)/(dx)=(-24-16)/(9+24)`

`(dy)/(dx)=(-40)/(33)`