Question

Can you charged particles at 1 m apart exert and 1 N force on each other. If the magnitude of each charges is doubled the force on each particle will be 1 N2 N4 N8 N

Answer 1

Given:

Distance between particles = 1 m

Force exerted = 1 N

Let's find the force on each particle if he magnitude of each charge is doubled.

Apply the Columb's Law:

`F=(kQ_1Q_2)/(r^2)`

Where:

F is the force

Q1 is the charge of particle 1

Q2 is the charge of particle 2

r is the distance between the particles.

Rewrite the equation for Q1Q2

`\begin{gathered} Q_1Q_2=(Fr^2)/(k) \\ \\ \\ Q_1Q_2=(1r^2)/(k) \end{gathered}`

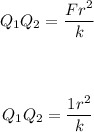
If the magnitude is doubled, we have:

Q1 = 1 x 2 = 2Q1

Q2 = 1 x 2 = 2Q2

Hence, we have:

`F=\frac{k2Q_12Q_2_{}}{r^2}`

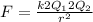
Rewrite the equation for Q1Q2:

`Q_1Q_2=(Fr^2)/(4k)`

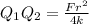
We have the equations for Q1Q2:

`\begin{gathered} Q_1Q_2=(r^2)/(k) \\ \\ Q_1Q_2=(Fr^2)/(4k) \end{gathered}`

Eliminate the equal sides of both eqautions and equate:

`(Fr^2)/(4k)=(r^2)/(k)`

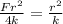
Make F subject of the equation:

Cross multiply

`\begin{gathered} Fr^2k=4r^2k \\ \\ \text{Divide both sides by r}^2k\colon \\ (Fr^2k)/(r^2k)=(4r^2k)/(r^2k) \\ \\ F=4\text{ N} \end{gathered}`

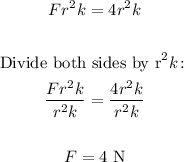
Therefore, when the magnitude of each charge is doubled, the force on each particle will be 4 N

ANSWER:

4 N