Question

16. (3 points) Determine the mass of a gold bar that has a density of 19.3 g/cm3 and is 2.72 cm high by 4.21 cm long by 2.98 cm deep. You must show all of your work for credit.

Answer 1

V - volume: 4.21×2,72×2,98 = 34,124576 cm3
d - density: 19.3 g/cm3
m - mass: ??
__________
d = m/V
m = d×V
m = 19.3×34,124576
m = 658,6g

:)

Answer 2

Answer: The mass of gold bar is 658.516 g

Step-by-step explanation:

To calculate the volume of cuboid, we use the equation:

`V=lbh`

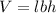
where,

V = volume of cuboid

l = length of cuboid = 4.21 cm

b = breadth of cuboid = 2.98 cm

h = height of cuboid = 2.72 cm

Putting values in above equation, we get:

`V=4.21* 2.98* 2.72=34.12cm^3`

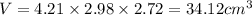
To calculate the mass of a substance, we use the equation:

`\text{Density of substance}=\frac{\text{Mass of substance}}{\text{Volume of substance}}`

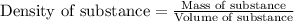
Density of gold bar =
`19.3g/cm^3`

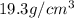
Volume of gold bar =
`34.12cm^3`

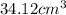
Putting values in equation 1, we get:

`19.3g/cm^3=\frac{\text{Mass of gold bar}}{34.12cm^3}\\\\\text{Mass of gold bar}=658.516g`

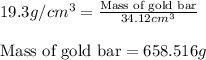
Hence, the mass of gold bar is 658.516 g