Question

If William wants to fill his empty fish tank, it will take 26 liters of water. If he puts 85 marbles on the bottom of the tank, it will take 20.9 liters of water.As in question 1, use these points to find the slope and write an equation of a line modeling the situation.Write your equation in the form y = mx + b.

Answer 1

The linear model is:

y= - 0.06x + 26

The question says:

1. It will take William 26 litres to fill up his fish tank

2. It will take William 20.9 litres to fill up his tank if he puts 85 marbles in the fish tank.

Therefore, we now have two scenarios:

1 with 85 marbles and 20.9 litres of water and 1 without any marble and 26 litres of water.

Notice that when the number of marbles was zero, the litres of water required to fill up the fish tank was 26 while when the marbles increased to 85, the litres of water the fish tank could hold became 20.9.

This means that as the number of marbles in the fish tank increases, the amount of water it can hold reduces. This leads to a negative rate relationship between the amount of water and the number of marbles

Therefore, this situation is good enough to create a linear model of the form:

`\begin{gathered} y=mx+b \\ \text{where m= slope of the model} \\ b=\text{value of y when x = 0} \end{gathered}`

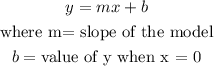
If we take the number of marbles in the fish tank as x

And we take the litres of water in the fish tank as y

In order to find the slope (m) of the linear model, we must use the formula:

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ y_2=\text{amount of water in second scenario=20.9 litres} \\ y_1=\text{amount of water in the first scenario=26 litres} \\ x_2=n\text{umber of marbles in the second scenario = 85 marbles} \\ x_1=n\text{umber of marbles in the first scenario= 0 marbles} \end{gathered}`

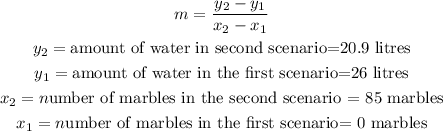
Thus, we can calculate the slope (m) as:

`m=(20.9-26)/(85-0)=-0.06`

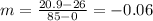
The slope (m) is negative because there is "a negative rate relationship between the amount of water and number of marbles" as stated earlier.

We have already stated that y-intercept (b) is the value when number of marbles in the fish

tank is zero.

Therefore,

`b=26`

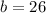
Thus, we can now write the linear model as:

`\begin{gathered} y=mx+b \\ m=-0.06 \\ b=26 \\ \\ \therefore y=-0.06x+26 \\ \\ x=\text{ number of marbles} \\ y=\text{litres of water} \end{gathered}`

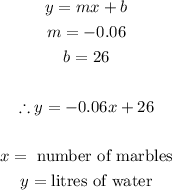
The linear model is:

y= - 0.06x + 26