Question

At Bank A, $600 is invested with an interest rate of 5% compounded annually. At Bank B, $500 is invested with an interest rate of 6% compounded quarterly. Which account will have a larger balance after 10 years? After 20 years?

Answer 1

The Solution:

It is given that

For Bank A:

`\begin{gathered} P=\text{ \$600} \\ R=5\text{ \% annually} \\ T=10\text{ yrs and T=20 yrs} \end{gathered}`

For Bank B:

`\begin{gathered} \text{ P=\$500} \\ \text{ R=6\% quarterly} \\ \text{ T=10yrs and 20 yrs} \end{gathered}`

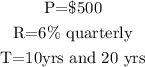
By the formula for the compound interest, we have

`\begin{gathered} A=P(1+(r)/(100\alpha))^(n\alpha) \\ \text{Where} \\ \alpha=\text{ number of periods per annum} \end{gathered}`

For Bank A:

`\begin{gathered} A=P(1+(r)/(100\alpha))^(n\alpha) \\ \text{ In this case,} \\ \alpha=1 \\ P=\text{ \$600} \\ r=\text{ 5\%} \\ n=10\text{ yrs, and 20 yrs} \end{gathered}`

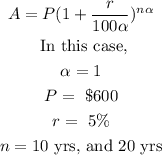
Substituting the corresponding values, we have

`\begin{gathered} A=600(1+(5)/(100*1))^((10*1)) \\ \\ A=600(1+0.05)^(10)=600(1.05)^(10)=977.337\approx\text{ \$977.34} \\ \end{gathered}`

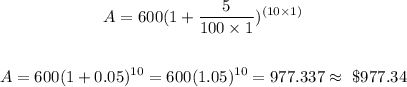
For Bank A for after 20 years:

`A=600(1.05)^(20)=1591.979\approx\text{ \$1591.98}`

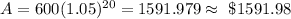
Similarly, for Bank B:

`\begin{gathered} A=P(1+(r)/(100\alpha))^(n\alpha) \\ \text{ In this case,} \\ \alpha=4 \\ P=\text{ \$500} \\ r=6\text{ \%} \\ n=10\text{ yrs, and 20 yrs} \end{gathered}`

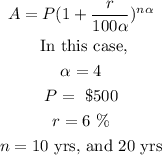
Substituting these values in the formula, we get