Question

Find the 34th percentile, P34, from the following data.12.712.913.917.117.619.319.520.622.323.424.624.824.925.625.926.0 26.827.128.729.030.130.831.032.132.933.234.035.135.539.040.642.543.643.844.948.445.746.347.147.9P34 =Calculator

Answer 1

DEFINITIONS:

Percentiles are the values below which a certain percentage of the data in a data set is found.

The formula to calculate the percentile of a given data is:

`n=(P)/(100)* N`

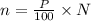
where N = number of values in the data set, P = percentile, and n = ordinal rank of a given value (with the values in the data set sorted from smallest to largest).

SOLUTION:

The total number of data provided in the table is 40. Hence, we have the following parameters:

`\begin{gathered} N=40 \\ P=34 \end{gathered}`

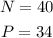
Therefore, we can calculate the rank to be:

`\begin{gathered} n=(34)/(100)*40 \\ n=0.34*40 \\ n=13.6 \end{gathered}`

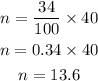
. Let us take the scores corresponding to the 13 th and 14th values.

`\begin{gathered} 13th\Rightarrow24.9 \\ 14th\Rightarrow25.6 \end{gathered}`

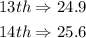
The integer part of the percentile will be the value of the 13th percentile: 24.9.

The decimal part will be calculated by finding the difference between the 13th and 14th positions, and multiplying this by the decimal:

`\begin{gathered} Difference\Rightarrow25.6-24.9=0.7 \\ Product\Rightarrow0.6*0.7=0.42 \end{gathered}`

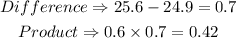
Therefore, the 13.6th position will be:

`\Rightarrow24.9+0.42=25.32`

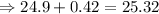
The 34th percentile approximately is 25.3