Question

How do I find the measure of angle X to the nearest 10th?

Answer 1

Given the right triangle MXN as shown below:

To evaluate the measure of angle X to the nearest tenth,

step 1: Identify the sides of the triangle.

In the triangle MXN, using the angle X as the angle of focus,

`\begin{gathered} XM\Rightarrow\text{adjacent} \\ MN\Rightarrow\text{opposite} \\ XN\Rightarrow\text{hypotenuse} \end{gathered}`

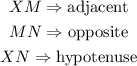
step 2: Evaluate the measure of angle X using trigonometric ratios.

From trigonometric ratios,

`\cos \theta=\frac{\text{adjacent}}{\text{hypotenuse}}`

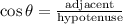
where

`\theta=X`

thus,

`\begin{gathered} \cos X=\frac{\text{adjacent}}{\text{hypotenuse}} \\ =(XM)/(XN) \\ \text{where } \\ XM=15,\text{ XN=}20 \\ \text{thus,} \\ \cos X=(15)/(20) \\ =0.75 \\ \Rightarrow X=\cos ^(-1)(0.75)^{} \\ =41.40962211 \\ \therefore X\approx41.4\degree\text{ (nearest tenth)} \end{gathered}`

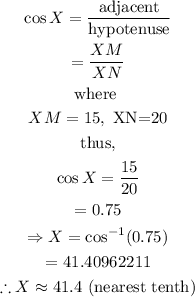
Hence, the measure of the angle X to the nearest tenth is 41.4 degrees.