Question

For each line find the slope between the 2 points given , simply each fraction to prove that the lines have a CONSTANT rate of change :1) Point T : 3) Point R :3) Point S :4) Slope of TR : 5) Slope of RS :6) Slope of TS :7) Describe the SLOPE of the line : 8) Therefore the CONSTANT rate of change is...?

Answer 1

For the information given in the statement and in the graph you have

*Point T has coordinates:

`(-5,0)`

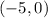
*Point R has coordinates:

`(1,2)`

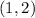
*Point S has coordinates:

`(7,4)`

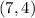
Now to find the slopes of the segments you can use the slope formula, that is

`\begin{gathered} m=(y_(2)-y_(1))/(x_(2)-x_(1)) \\ \text{ Where m is the slope of the line and} \\ (x_1,y_1),(x_2,y_2)\text{ are two points through which the line passes} \end{gathered}`

So, the slope of TR is

`\begin{gathered} (x_1,y_1)=(-5,0) \\ (x_2,y_2)=(1,2) \end{gathered}`
`\begin{gathered} m=(2-0)/(1-(-5)) \\ m=(2)/(1+5) \\ m=(2)/(6) \\ \text{ Simplifying} \\ m=(2\cdot1)/(2\cdot3) \\ m=(1)/(3) \end{gathered}`

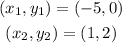
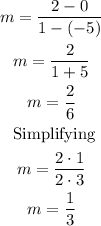
Now, the slope of RS is

`\begin{gathered} (x_1,y_1)=(1,2) \\ (x_2,y_2)=(7,4) \end{gathered}`
`\begin{gathered} m=(4-2)/(7-1) \\ m=(2)/(6) \\ m=(1)/(3) \end{gathered}`

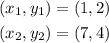
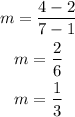
Now, the slope of TS is

`\begin{gathered} (x_1,y_1)=(-5,0) \\ (x_2,y_2)=(7,4) \end{gathered}`
`\begin{gathered} m=(4-0)/(7-(-5)) \\ m=(4)/(7+5) \\ m=(4)/(12) \\ \text{ Simplifying} \\ m=(4\cdot1)/(4\cdot3) \\ m=(1)/(3) \end{gathered}`

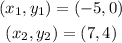
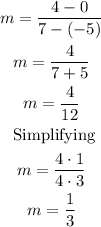
For point 7, you know that a single line passes through two points, and since the segments, TR, RS, and TS have the same slope, that is, 1/3 then the SLOPE of the line is 1/3.

For point 8, you know that the constant rate of change with respect to the variable x of a linear function is the slope of its graph. Therefore, the CONSTANT rate of change is 1/3.