Question

A boat drives towards a lighthouse whose windows are located 60 m above sea level. From a window in the lighthouse you can see at 14.58 the boat at an angle of 9.8∘ below the horizontal plane. At 15.01 is the corresponding angle 32.4∘. How fast is the boat traveling? (Answer in km/h).

Answer 1

We have to draw a sketch to understand the question

To find the speed of the boat we have to find the distance in the sketch

Let me put letters for the points to be easy

We need to find BC using the trigonometry ratio

`tan9.8=(AB)/(BD)`

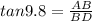
AB = 60 m

`tan9.8=(60)/(BD)`

Switch BD with tan 9.8

`BD=60tan9.8`

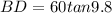
Now, we need to find BC using the same ratio but with an angle of measure 32.4 degrees

`\begin{gathered} tan32.4=(AB)/(BC) \\ \\ tan32.4=(60)/(BC) \\ \\ BC=60tan32.4 \end{gathered}`

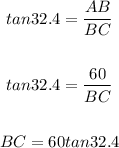
To find the distance subtract BC from BD

`\begin{gathered} D=BD-BC \\ D=\lvert{60tan9.8-60tan32.4}\rvert \end{gathered}`

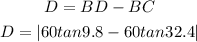
The time is from 14.58 to 15.01

There are 3 minutes between them

1 h = 60 min

1 km = 1000 m

Then we will divide the distance by 1000 and the time by 60

`\begin{gathered} S=(D)/(T) \\ \\ S=\frac{\frac{\lvert{60tan9.8-60tan32.4}\rvert}{1000}}{(3)/(60)} \\ \\ S=0.55\text{ km/h} \end{gathered}`

The speed of the boat is about 0.55 km/h to the nearest 2 decimal places