Question

If a gardener fences in the total rectangular area shown in theillustration instead of just the square area, he will need twiceas much fencing to enclose the garden. How much fencing willhe need?

Answer 1

- The formula for finding the Perimeter of a square is:

`\begin{gathered} P=4x \\ where, \\ x=\text{ The dimension of the square} \end{gathered}`

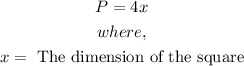
- The perimeter of a rectangle is:

`\begin{gathered} P=2(l+b) \\ where, \\ l=\text{ The length of the rectangle} \\ b=\text{ The width of the rectangle} \end{gathered}`

- The perimeter of the square garden will be:

`P_1=4x`

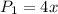
- The Perimeter of the whole rectangular garden is:

`\begin{gathered} P_2=2([26+x]+x) \\ where, \\ l=26+x \\ b=x \\ \\ \therefore P_2=2(26+2x) \\ \\ P_2=52+4x \end{gathered}`

- We are also told that if the gardener is to fence the whole rectangular garden, he'd use twice as much fencing.

- This implies that

`P_2=2* P_1`

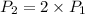
- Substituting the expressions for P2 and P1 into the above expression, we can find the value of x and subsequently, the total amount of fencing he will need.

- This is done below:

`\begin{gathered} P_2=2* P_1 \\ P_2=52+4x \\ P_1=4x \\ \\ 52+4x=2(4x) \\ 52+4x=8x \\ \text{ Subtract 4x from both sides } \\ 52=8x-4x \\ 4x=52 \\ Divide\text{ both sides by 4} \\ \\ (4x)/(4)=(52)/(4) \\ \\ \therefore x=13 \end{gathered}`

- Now that we have the value of x, we can proceed to find the total amount of fencing needed.

- This is

`\begin{gathered} P=52+4x \\ x=13 \\ \\ P=52+4(13) \\ \\ P=104ft \end{gathered}`

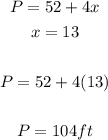
Final Answer

The total fencing needed is 104 ft