Question

What is the equation of the quadratic graph with a focus of (-4, -5/4) and a directrix of y= 27/4

Answer 1

The equation of the quadratic graph with a focus of (-4, -5/4) and a directrix of y= 27/4 is y = -5/4 + (1/19.6) or y = -5/4 - (1/19.6).

Step-by-step explanation:

The equation of a quadratic graph with a focus and a directrix can be found using the formula x = h and y = k ± (1/(4a)), where (h, k) is the coordinates of the focus and a is the coefficient of the quadratic term. In this case, the focus is (-4, -5/4) and the directrix is y = 27/4.

Plugging the values into the formula, we get x = -4 and y = -5/4 ± (1/(4a)). To find the value of a, we can use the equation of the directrix. Since the directrix is y = 27/4, we can set it equal to the equation of the parabola, which gives us -5/4 ± (1/(4a)) = 27/4. Solving for a, we find that a = 4.90.

Substituting the value of a into the equation of the parabola, we have y = -5/4 ± (1/(4 * 4.90)). Simplifying further, we get y = -5/4 ± (1/19.6). Therefore, the equation of the quadratic graph is y = -5/4 + (1/19.6) or y = -5/4 - (1/19.6).

Answer 2

check the picture below.

now, notice the "p" distance, from the focus or directrix to the vertex.

bear in mind the vertex is halfway between those two fellows, so... we simply need to check the length from the focus to the directrix, get half of that, add it to either the focus y-coordinate or the directrix, in order to get the y-coordinate of the vertex, so let's do so.


`\bf \stackrel{focus}{\cfrac{5}{4}}+\stackrel{directrix}{\cfrac{27}{4}}\implies \cfrac{32}{4}\implies 8`

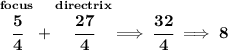
so, there are 8 units in between them, half that is just 4, let's add 4 to say hmmm -5/4 to see where it ends.


`\bf -\cfrac{5}{4}+4\implies \cfrac{11}{4}\implies \boxed{2(3)/(4)} \\\\\\ \textit{so, the vertex is really at }\left( -4~,~ (11)/(4)\right)`

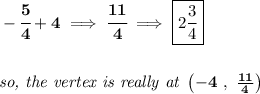
alrite, now, notice, the focus point is below the directrix, is a vertical parabola opening downwards, as you already saw in the picture anyway. That simply means that the "p" value is negative, so is really -4.

now, let's plug those values in the focus-point form of a parabola.


`\bf \textit{parabola vertex form with focus point distance}\\\\ \begin{array}{llll} (y-{{ k}})^2=4{{ p}}(x-{{ h}}) \\\\\boxed{ (x-{{ h}})^2=4{{ p}}(y-{{ k}}) }\\ \end{array} \qquad \begin{array}{llll} vertex\ ({{ h}},{{ k}})\\\\ {{ p}}=\textit{distance from vertex to }\\ \qquad \textit{ focus or directrix} \end{array}\\\\ -------------------------------\\\\`


`\bf \begin{cases} h=-4\\ k=(11)/(4)\\ p=-4 \end{cases}\qquad [x-(-4)]^2=4(-4)\left( y-(11)/(4) \right) \\\\\\ (x+4)^2=-16\left( y-(11)/(4) \right)\implies -\cfrac{1}{16}(x+4)^2=y-\cfrac{11}{4} \\\\\\ -\cfrac{1}{16}(x+4)^2+\cfrac{11}{4}=y\implies -\cfrac{1}{16}(x+4)^2+2(3)/(4)=y`