Question

The period of f(x)=cos x is 2π. What is the period of g?

Answer 1

The answer is: Option C

We have been given the function:

`\begin{gathered} g(x)=-5\cos (8x-(\pi)/(2))+3 \\ \end{gathered}`

In order to find the period for this equation, we must compare it with the standard waveform equation.

This standard equation is given below:

`\begin{gathered} y=A\cos (\omega x+k)+B \\ \text{where,} \\ \omega=(2\pi)/(T) \\ T=\text{period of oscillation} \\ \\ \therefore y=A\cos \mleft(\mright.(2\pi)/(T)x+k)+B \\ \end{gathered}`

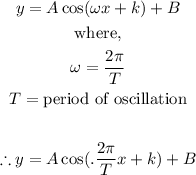
When we compare the equation from the question with this standard form, we get:

`\begin{gathered} 8x=(2\pi)/(T)x \\ \\ \therefore(2\pi)/(T)=8 \\ \\ T=(2\pi)/(8)=(2*\pi)/(2*4)=(\pi)/(4) \\ \\ \therefore\text{Period(T)}=(\pi)/(4)\text{ (Option C)} \end{gathered}`