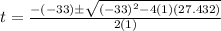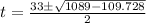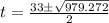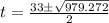Question

A rocket is launched and the quadratic function h(t) = -5t^2+ 165t relates the height (h) in meters to seconds (t) after launch. When will the rocket be 450 feet above the ground? (Hint...twice!!!)

Answer 1

Given:

`h(t)=-5t^2+165t`

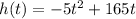
where h is the height in meters and t is the second in seconds.

Required:

We need to find the time when the rocket is 450 feet height from the ground.

Step-by-step explanation:

We need to convert 450 feet into meters.

`\text{We know that 1 foot = 0.3048 meters.}`

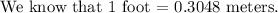
Multiply both sides by 450.

`450\text{ }*\text{1 foot = 450 }*\text{ 0.3048 meters.}`

`450\text{ }* fee\text{t = 137.16 meters.}`

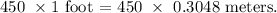
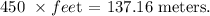
Substitute h(t)= 137.16 meters in the given equation to find the value of t.

`137.16=-5t^2+165t`

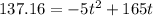
Solve for t.

`5t^2-165t+137.16=0`

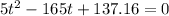
Divide both sides of the equation by 5.

`(5t^2)/(5)-(165t)/(5)+(137.16)/(5)=0`

`t^2-33t+27.432=0`

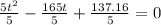
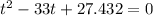
which is of the form.

`at^2+bt+c=0`

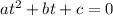
where a =1, b=-33 and c =27.432.

Consider the quadratic formula.

`t=(-b\pm√(b^2-4ac))/(2a)`

Substitute a =1, b=-33, and c =27.432 in the formula to find the value of t.

`t=(-(-33)\pm√((-33)^2-4(1)(27.432)))/(2(1))`

`t=(33\pm√(1089-109.728))/(2)`

`t=(33\pm√(979.272))/(2)`

`t=(33\pm√(979.272))/(2)`