Answer-
The inverse of
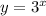 is
is
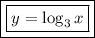
Solution-
The given function is,
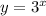
We can get the inverse by interchanging he variable x and y among themselves and then separating each variables.
So in the inverse would be,
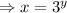
Taking log of both sides,
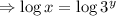
As,
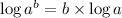
Applying the same,

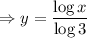
As,

Applying the same,

Therefore, the inverse of
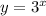 is
is
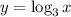 .
.