Question

How many photons are emitted during 9.67 s of operation of a red laser pointer? The device outputs 2.71 Watts at a 684.82 nm wavelength.

Answer 1

We are asked to determine the number of photons emitted by a laser pointer. To do that we will first determine the energy carried by each of the photons using the following formula:

`E_p=(hc)/(\lambda)`

Where:

`\begin{gathered} E_p=\text{ energy per photon} \\ h=\text{ Plank's constant} \\ c=\text{ speed of light} \\ \lambda=\text{ wavelength} \end{gathered}`

Plank's constant is given by:

`h=6.63*10^(-34)(m^2kg)/(s)`

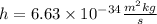
The speed of light is given by:

`c=3*10^8(m)/(s)`

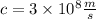
Now, we substitute the values in the equation:

`E_p=((6.63*10^(-34)(m^2kg)/(s))(3*10^8(m)/(s)))/(684.82*10^(-9)m)`

Solving the operations:

`E_p=2.9*10^(-19)J`

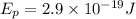
Now, we determine the energy emitted by the laser pointer using the following formula:

`E=Pt`

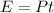
Where "P" is power, and "t" is time:

`E=(2.71W)(9.67s)=26.2J`

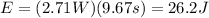
Now, to determine the total number of electrons we use the fact that the energy per photon multiplied by the number of photons must be equal to the total energy emitted. Therefore, we have:

`E=nE_p`

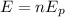
Where "n" is the number of photons. Dividing both sides by the energy per photon:

`(E)/(E_p)=n`

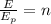
Now, we plug in the values:

`(26.2J)/(2.9*10^(-19)J)=n`

Solving the operations:

`9*10^9=n`

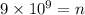
Therefore, 9 x 10^9 photons are emitted.