Question

The side of a square is measured to be 12 ft with a possible error of ±0.1 ft. Use differentials to estimate the error in the calculated area. Include units in your answer

Answer 1

±2.4 square feet

Explanation:

To estimate the error in the calculated area of the square when the side is measured as 12 ft with a possible error of ±0.1 ft, we can use differentials.

Let the area of a square be given by the formula:

`\large\boxed{y = x^2}`

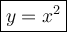
where:

• y is the area.
• x is the length of one side.

Differentiate the equation for area with respect to x:

`\frac{\text{d}y}{\text{d}x}=2x`

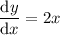
Rearrange to isolate dy:

`\text{d}y=2x\cdot \text{d}x`

Here, dx is the change in the side length, and we are estimating the change in area (dy) due to this change in x.

The measurement of the side length is accurate to within 0.1 ft, so:

`-0.1 \leq \text{d}x\leq0.1`

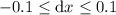
As dy = 2x · dx, this means that:

`2x\cdot (-0.1)\leq\text{d}y\leq2x\cdot (0.1)`

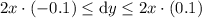
Using the given side length of 12 ft, we can estimate the error in the calculated area by substituting x = 12 into the inequality:

`2(12)\cdot-0.1 \leq \text{d}y\leq 2(12)\cdot 0.1`

`24\cdot-0.1 \leq \text{d}y\leq24\cdot 0.1`

`-2.4 \leq \text{d}y\leq 2.4`

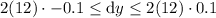
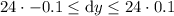
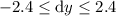
Therefore, the estimated error in the calculated area is ±2.4 square feet.