Question

I need to find area, circumference, arc length and area of a sector

Answer 1

In the given figure of circle :

AC is the diameter

AC = 46

Since, Diameter is the twice of radius. So,

Radius = Diameter/2

Radius = 46/2

Radius = 23

Area of Circle:

The area of circle is express as :

`\text{ Area of Circle = }\Pi(radius)^2`

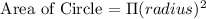
Substitute the value of radius = 23

`\begin{gathered} \text{ Area of Circle = }\Pi(radius)^2 \\ \text{ Area of Circle =}\Pi(23)^2 \\ \text{ Since }\Pi=3.14 \\ \text{Area of Circle =}3.14*23*23 \\ \text{Area of Circle =}1661.06 \end{gathered}`

Area of Circle is 1661.06

Circumference of Circle :

The circumference of circle is express as :

`\text{ Circumference of circle = 2}\Pi(radius)`

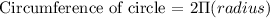
Substitute the value of radius =23

`\begin{gathered} \text{ Circumference of circle = 2}\Pi(radius) \\ \text{ Since }\Pi=3.14 \\ \text{Circumference of circle = 2}*3.14*23 \\ \text{Circumference of circle = }144.44 \end{gathered}`

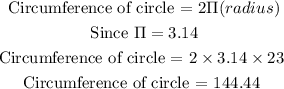
Circumference of circle is 144.44

Arce Length:

The expression for the arc length is

`\text{ Arc Lenth = radius (Angle substended by the arc)}(\Pi)/(180)`

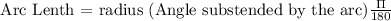
Since Angle AEB and DEC are vertically opposite angle

Angle AEB = Angle DEC = 63

Substitute the value and simplify:

`\begin{gathered} \text{ Arc Lenth = radius (Angle substended by the arc)}(\Pi)/(180) \\ \text{ Arc Length=23(63}^o)(\Pi)/(180) \\ \text{Arc length =}23*1.099 \\ \text{Arc Length=}25.277 \end{gathered}`

Arc Length = 25.277

Area of sector:

The expression for the area of sector is :

`\text{ Area of sector =}(\theta)/(360)*\Pi(radius)^2`

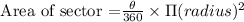
Substitute the value

`\begin{gathered} \text{ Area of sector =}(\theta)/(360)*\Pi(radius)^2 \\ \text{ Area of sector =}(63)/(360)*3.14(23)^2 \\ \text{ Area of sector}=0.175*1661.06 \\ \text{ Area of sector = }290.68 \end{gathered}`

Area of Sector DEC is 290.68