Question

Question 6This figure is made from a part of a square and a part of a circle.a. What is the perimeter of this figure to the nearest unit.b. What is the area of this figure to the nearest square unit.

Answer 1

Given:

square with sides 10 x 10

circle with radius 5 units.

shape is 3/4 square and 1/4 circle.

Find: perimeter and area of the figure

Solution:

Let's solve the perimeter first.

The perimeter of a square is four times the side of its length,

`P=4s`

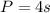
Since the length of the side is 10 units, the perimeter of the full square is:

`P=4(10)=40units`

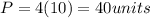
Since the figure is only 3/4 square, then the perimeter of the square part of the shape is 3/4 times 40 units = 30 units only.

Now, let's solve for the circumference of the circle. Formula is:

`C=2\pi r`

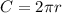
Radius of the circle is 5 units and π ≈ 3.14. Let's plug this in to the formula.

`\begin{gathered} C=2(3.14)(5)=31.4units \\ \text{shape is 1/4 circle only. } \\ 31.4units*(1)/(4)=7.85units \end{gathered}`

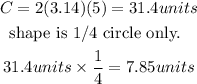
Hence, the circumference of the circle part is 7.85 units only.

Therefore, the perimeter of the figure is 30 units + 7.85 units = 37.85 units or approximately 38 units.

Let's now solve for the area.

Let's solve the area of the full square first then, multiply the answer to 3/4 since our figure is only 3/4 square.

`\begin{gathered} A=s^2=10^2=100sq.units \\ 100sq.units*(3)/(4)=75sq.units \end{gathered}`

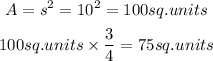
Now, let's solve for the area of the circle part. We will use the area for circle formula then, multiply it to 1/4 since the figure is only 1/4 circle.

`\begin{gathered} A=\pi r^2=(3.14)(5^2)=3.14(25)=78.5sq.units \\ 78.5sq.units*(1)/(4)=19.625sq.units \end{gathered}`

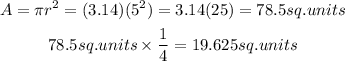
The area of the 3/4 square is 75 sq units while the area of the 1/4 circle is 19.625 sq units, hence, the total area of the figure is (75 + 19.625) 94.625 square units or approximately 95 square units.